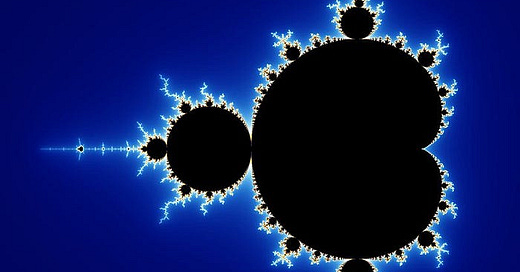
Can A Mathematical Equation Explain Creation?
“The Thumbprint Of God”, Plato, Self-similarity, and a reason for the world around us

There’s something mind-blowing hidden within the picture above. But put it aside for now. I have an important question to ask.
How many times have you looked around you and asked “why” or “how?” For instance, how did this complicated world of people, animals, plants, and elements come into existence? But it’s not only your question.
It’s one every philosopher, and likely every human being throughout time has asked. And the question is a worthy one.
In his documentary The Secret Life of Chaos, theoretical physicist Jim Al-Khalili tries to answer it. He reveals ninety-nine percent of the human body is a mixture of air, water, coal, and chalk, with the combination costing only dollars to make.
Yet, the simple elements become us: a complex thinking, loving, destroying, and creating creature. It’s spectacular when you think about it. Philosophers thought so too.
It forced Plato to think more ethereally, focusing on perfect versions of what we see in the world. He called them “forms.” While a triangle we draw may be flawed, the concept of “triangle” is perfect and immortal. It also pushed him heavily into mathematics and geometry — the ultimate “form” or concept.
But as Plato could tell you, the world doesn’t resemble the “forms.” Al-Khalili picks up a random rock at the beach, and it’s neither square, rectangle, nor sphere — more a mix of all. The word “random” fits it perfectly.
This randomness presents trouble. According to Al-Khalili, Newtonian physics sees the universe similar to a clock, whose movements can be predicted and anticipated with a better formula. Yet, like Plato’s forms, it doesn’t work that way.
Although there is a mathematical formula that can somewhat explain the world we see around us. Strangely, it’s in the picture above. The complexity we see is simplicity on an infinite loop of sorts.
Forgive my vagueness, I haven’t made the picture above clear enough just yet. We need a couple reference points to bring the image into view. We’ll start with Alan Turing, then take a trip to Russia.
Self-Organization Without Direction
I’m sure you recognize Alan Turing’s name. Maybe due to the Turing Test for artificial intelligence. Or you’ve seen the movie the Imitation Game, which is based on Turing’s work breaking Nazi codes. But this is only one piece of Turing.
Perhaps his greatest discovery involved one of the biggest puzzles of all: how cells develop. It’s called morphogenesis. Simply put, all cells within an early embryo are all the same. Yet in development, suddenly some cells become skin, others eyes, and the rest something else.
Oddly, it happens spontaneously with no direction. But how? Well, Turing had a truly unique idea on how to figure it out. He used equations generally used in physics to describe biological processes in his 1952 paper The Chemical Basis of Morphogenesis.
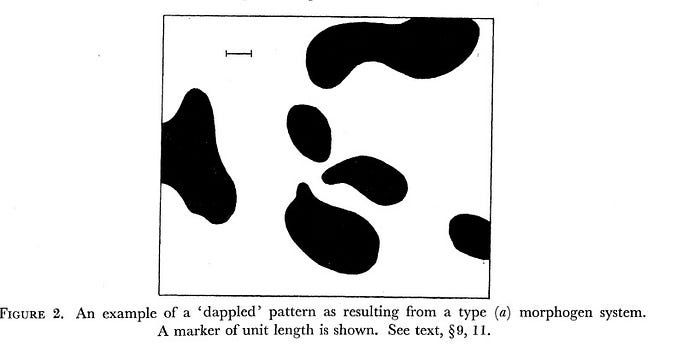
In essence, he used math to explain natural patterns like stripes, spirals, or even the “dapples” on a cow’s skin. Al-Khalili likens it to wind blowing sand into self-organized patterns. Chemicals moving across an embryo have the same affect, transforming homogeneous cells.
Meanwhile about the same time in the Soviet Union — with no knowledge of Turing’s work — Soviet chemist Boris Belousov performed an experiment. He mixed various chemicals together and his solution changed color. Obviously, not ground-breaking.
Then, something weird happened. It changed back. Afterwards, it reverted again and continued to oscillate colors. But the solution provided one more surprise when it wasn’t mixed. If left idle, patterns appeared in the mixture on their own, generating random shapes.
It was Turing’s paper in a Petri dish — self organization without direction. It became known as the Belousov–Zhabotinsky reaction. And Both Turing and Belousov’s work foreshadows what’s to come
It has to do with the original picture we spoke about. Hidden within is an explanation of how the simplest materials can turn into complex creatures like you and me. We find the key to the puzzle at IBM.
Mandelbrot And Fractals
Benoit Mandelbrot — like Turing — also had a great interest in patterns, science, and mathematics. But there was a problem. In his 2010 Ted Talk, he referred to life and the universe as “a mess,” and the greater world around as having a “roughness.”
Seemingly, no pattern, or order.
This curious nature of the world pulled him from academia to an environment where he could study it — IBM. The organization’s raw computer power enabled him to experiment. Although the computers showed him something unexpected: there was order where none appeared to exist.
Mandelbrot created a term “fractal,” and it established a new type of geometry. The Encyclopedia Britannica defines fractal (geometry) as:
“Fractals possess the property of self-similarity... A self-similar object is one whose component parts resemble the whole. This reiteration of details or patterns occurs at progressively smaller scales and can, in the case of purely abstract entities, continue indefinitely, so that each part of each part, when magnified, will look basically like a fixed part of the whole object…This fractal phenomenon can often be detected in such objects as snowflakes and tree barks.”
He found these patterns everywhere. In the branches of trees, dunes of sand, human blood vessels and the lungs, geographical landmarks on maps, and the structure of the heavens. So, he created a formula to describe it.
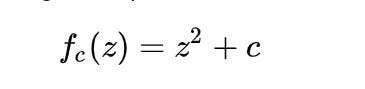
You could write an entire paper on this equation, but to simplify, it replicates a repeating pattern to infinitely smaller scales for eternity. Words can’t do it justice though. It’s better to see it in action through animation in all its trippy glory. Get prepared.
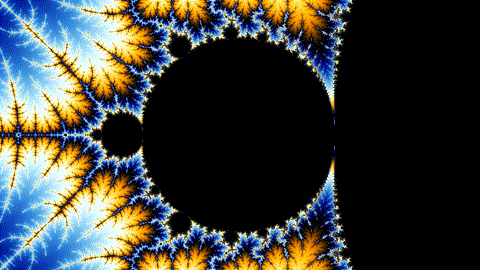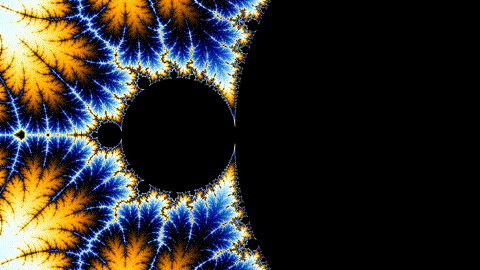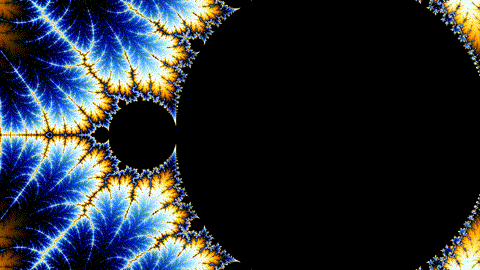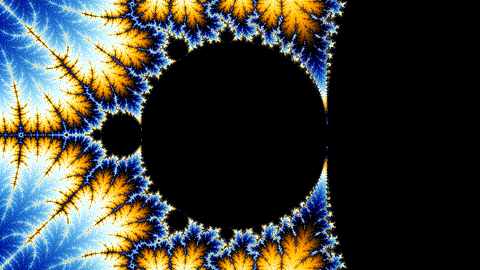
Don’t stare at it too long, it’ll put you in a trance. This pictorial is an explanation of Turing’s Morphogenesis, Belousov’s chemicals, and the complexity of nature and us. In truth, it’s simple patterns repeating — infinitely.
At this point, I’m sure you have a question. Does this mean we can actually calculate the randomness of the world we see around us? Well, not exactly.
Chaos And Patterns
Al-Khalili reveals that even the simplest equations can be thrown off by minuscule factors that can’t be calculated. Science calls this chaos. It was originally discovered by Edward Lorenz, a meteorologist attempting to calculate future air currents.
He couldn’t. Lorenz found that the smallest change in formulas could alter his weather calculations exponentially as patterns replicate. He coined the term “butterfly effect.” As in the flap of a butterfly’s wings on the other side of the planet could cause a tornado here.
These are feedback loops. So, while you can see many patterns repeated in the universe around you, it’s not always guaranteed. Even the simplest equations can be subject to these loops. But in many ways chaos and pattern are part of the greater equation of life. Not opposites; more like coworkers.
Also, evolution works to promote random changes to patterns which serve life in a better way. Almost like…there’s a plan in the randomness. If you didn’t think this was weird already, get ready.
A Creator Hidden In The Numbers
“One of the things that makes people so uncomfortable about this idea of spontaneous pattern formation is that somehow or other, you don’t need a creator. But perhaps a really clever designer — what he would do is to kind of treat the universe like a giant simulation. Where you set some initial condition and just let the whole things spontaneously happen in all of its wonder and all its beauty.”
— Dr. Andrea Sella (University College London) — The Secret Life of Chaos
I earlier mentioned Plato considered mathematics to be his ultimate form. In fact, he treated it like a religion. And why wouldn’t he? The concepts he found in geometry required higher thought, never grew old, and were perfect in every way.
A few thousand years afterwards, Father Pierre Teilhard de Chardin, had similar thoughts of evolution. The renowned archeologist believed consciousness itself evolved. Eventually, humanity would grow into a united collective, enabling itself to be one with God.
While the scientists in the documentary dance around the idea, they also point to the endless patterns we see repeated in nature. In many ways, it’s bizarre. Areas you think are completely random, aren’t that way.
I couldn’t help feeling what Dr. Sella described in his comment above after watching Mandelbrot’s set, the patterns in the Petri dish, and Turing’s dapples. It’s like some hidden hand pushed a snowball down a hill, leaving it to gather force. Obviously, this is just speculation.
Depending upon your worldview, everything you’ve read may prove or disprove a hidden creative force at work. But one thing is certain. We have a better idea how to answer that ultimate question.
How did this complicated world of people, animals, plants, and elements come into existence? Through simple patterns repeated infinitely, curated by chaos.
- Originally published on Medium 9/4/22